Complete graph

Complete graph
K₇, a complete graph with 7 vertices
Vertices	n
Edges	n(n − 1) / 2
Diameter	1
Girth	3 if n ≥ 3
Automorphisms	n! (S_n)
Chromatic number	n
Chromatic index	n if n is odd n-1 if n is even
Properties	(n-1)-regular Symmetric graph Vertex-transitive Edge-transitive Unit distance Strongly regular Integral
Notation	$K_n$

In the mathematical field of graph theory, a complete graph is a simple graph in which every pair of distinct vertices is connected by a unique edge.

1 Properties
2 Geometry and topology
3 Examples
4 Applications
5 References
6 External links

Properties

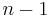The complete graph on n vertices has n(n-1)/2 edges, and is denoted by $K_n$ (from the German komplett^[1]). It is a regular graph of degree $n-1$ . All complete graphs are their own cliques. They are maximally connected as the only vertex cut which disconnects the graph is the complete set of vertices. The complement graph of a complete graph is an empty graph.

Geometry and topology

A complete graph with n nodes represents the edges of an (n-1)-simplex. Geometrically K₃ forms the edge set of a triangle, K₄ a tetrahedron, etc. The Császár polyhedron, a nonconvex polyhedron with the topology of a torus, has the complete graph K₇ as its skeleton. Every neighborly polytope in four or more dimensions also has a complete skeleton.

K₁ through K₄ are all planar graphs. However, every planar drawing of a complete graph with five or more vertices must contain a crossing, and the nonplanar complete graph K₅ plays a key role in the characterizations of planar graphs: by Kuratowski's theorem, a graph is planar if and only if it contains neither K₅ nor the complete bipartite graph K_3,3 as a subdivision, and by Wagner's theorem the same result holds for graph minors in place of subdivisions.

Examples

Complete graphs on n vertices, for 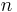$n$ between 1 and 12, are shown below along with the numbers of edges:

$K_1: 0$	$K_2: 1$	$K_3: 3$	$K_4: 6$

$K_5: 10$	$K_6: 15$	$K_7: 21$	$K_8: 28$

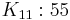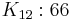$K_9: 36$	$K_{10}: 45$	$K_{11}: 55$	$K_{12}: 66$

Applications

Since a complete graph contains all n(n-1)/2 possible edges, it gives a quadratic upper bound on the number of connections in large connected systems like social and computer networks.

References

↑ David Gries and Fred B. Schneider, A Logical Approach to Discrete Math, Springer, 1993, p 436.

External links

Counting Paths and Cycles in Complete Graphs. Results are available Mehdi Hassani, Cycles in graphs and derangements, Math. Gaz. 88(March 2004) pp. 123-126 (reprint) or here

Weisstein, Eric W., "Complete Graph" from MathWorld.